Андре́й Никола́евич Колмого́ров
Андрей Николаевич Колмогоров - один из основоположников современной теории вероятностей, им получены фундаментальные результаты в топологии, геометрии, математической логике, классической механике, теории турбулентности, теории сложности алгоритмов, теории информации, теории функций, теории тригонометрических рядов, теории меры, теории приближения функций, теории множеств, теории дифференциальных уравнений, теории динамических систем, функциональном анализе и в ряде других областей математики и её приложений.
В период Великой Отечественной войны Андрей Николаевич по заданию Главного артиллерийского управления, используя свои работы по математике в области теории вероятностей, дал определение наивыгоднейшего рассеивания артиллерийских снарядов. Полученные им результаты помогли повысить меткость стрельбы и тем самым усилить действие артиллерии, которую заслуженно называли «богом войны». Его разработки по математической теории вероятностей использовались для определения наилучших методов нахождения самолетов, подводных лодок противника и для указания путей, позволяющих избежать встречи с подлодками врага. Во всем этом большая заслуга математической, школы академика А.Н. Колмогорова.
Лабиринт
Этот лабиринт юный Лью́ис Кэ́рролл нарисовал для своих домашних в рукописном журнале «Мишмаш». Сумеете ли вы выбраться из него?
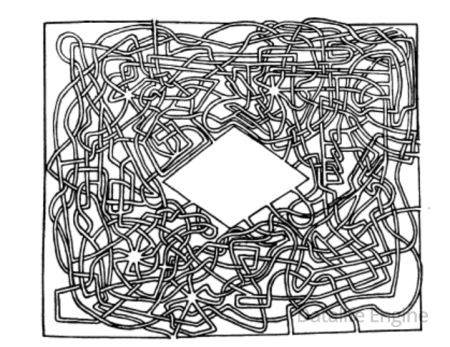
Источник: Научно-популярное издание. Кэрролл Льюис. Логическая игра
Сколько секунд потребуется шестому спортсмену?
Представление опыта педагогической деятельности по использованию техник визуализации на уроках математики
Задача Фибоначчи о размножении кроликов
Пусть в огороженном месте имеется пара кроликов (самка и самец) в первый день января. Эта пара кроликов производит новую пару кроликов в первый день февраля и затем в первый день каждого следующего месяца.
Каждая новорожденная пара кроликов становится зрелой уже через месяц и затем через месяц дает жизнь новой паре кроликов.
Сколько пар кроликов будет в огороженном месте через 12 месяцев с начала размножения? Источник: https://logiclike.com/math-logic/interesno-polezno/famous-math-puzzles
Источник: https://logiclike.com/math-logic/interesno-polezno/famous-math-puzzles
Научно-популярный физико-математический журнал для школьников и студентов "Квант"
Научно-популярный физико-математический журнал для школьников и студентов![]()
![]()
сайт
Календарь знаменательных дат. Апрель
Иоганн Карл Фридрих Гаусс
(30 апреля 1777 - 23 февраля 1855)

Ему принадлежат основополагающие исследования почти во всех областях математики: теории чисел, геометрии, анализе, алгебре, теории вероятности, а также в астрономии, геодезии, небесной механике, физике и теории магнетизма. За всестороннее и глубокое изучение науки он получил неофициальное звание короля математики.
В честь Гаусса названы:
- кратер на Луне;
- малая планета № 1001 (Gaussia);
- Гаусс — единица измерения магнитной индукции в системе СГС; сама эта система единиц часто именуется гауссовой;
- одна из фундаментальных астрономических постоянных — постоянная Гаусса;
- награда за выдающиеся достижения в прикладной математике, присуждаемая раз в 4 года на Международном конгрессе математиков;
- вулкан Гауссберг в Антарктиде.
Поздравляем победителей!
Поздравляем с победой
в городской олимпиаде
по учебному предмету "Математика"
Савицкую Татьяну (диплом 2 степени),
Савицкую Марину (диплом 3 степени)
Носарева Ивана (диплом 3 степени).
Желаем дальнейших успехов!

ХXXII ОЛИМПИАДА ПО МАТЕМАТИКЕ, ИНФОРМАТИКЕ и КРИПТОГРАФИИ
ХXXII ОЛИМПИАДА ПО МАТЕМАТИКЕ, ИНФОРМАТИКЕ и КРИПТОГРАФИИ
для учащихся
учреждений среднего образования
(факультет прикладной математики и информатики БГУ)
Участие школьников в олимпиаде бесплатное.
Олимпиада проводится в два тура (первый – заочный).
Прием работ первого тура – до 12 апреля 2023 г.
Заключительный тур олимпиады пройдет в течение двух дней в БГУ на факультете прикладной математики и информатики 29-30 апреля 2023 года.
 информация
информация
Поздравляем победителей!


 Поздравляем с победой
Поздравляем с победой (диплом 3 степени)
в заключительном этапе республиканской олимпиады
по учебному предмету "Математика"
Окуневу Анастасию,
учащуюся 8 "А" класса!!!







