Программа дня числа  ПИ

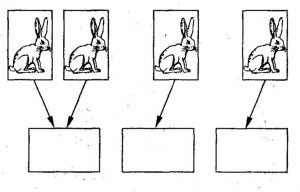
Самая распространенная формулировка принципа Дирихле, как ни странно, связана с кроликами:

если в n клетках сидит n+1 кролик, то по крайней мере в одной клетке сидит не менее двух кроликов. 

Если в первую клетку посадить учеников, которые не сделали ни одной ошибки, во вторую - сделавших две ошибки и т.д., а в тринадцатую посадить Вову, то решить задачу можно опять методом от противного:

Пусть среди класса нет учеников, сделавших одинаковое количество ошибок. Тогда в каждой клетке максимум 2 ученика. Т.к. клеток всего 14 (в последней сидит один Вова), то суммарное количество учеников не может превышать 13*2+1=27 человек. Мы пришли к противоречию, т.к. диктант писало 30 ребят.

(13.02.1805 - 05.05.1859)

• Он ввёл такое понятие, как «условная сходимость» и определил её признак;
• Доказал теорему о прогрессии;
• Высказал принцип Дирихле;
• Значительно развил теорию потенциала.

2025 ГОД С ТОЧКИ ЗРЕНИЯ МАТЕМАТИКИ

1. Квадратное число:  45²=2025;  (20+25)²=2025; 9²×5²=2025;  3²×15²=2025. 

Разложение на простые множители выглядит так: 2025=5²×3⁴.
Сумма цифр числа 2025 равна 9, что также является квадратом (3²).
2. Кубическое число: 2025 можно представить как сумму кубов всех цифр от 0 до 9: 0³+1³+2³+3³+4³+5³+6³+7³+8³+9³=2025.

3. У числа 2025 есть 15 делителей, и оно делится на 15.

Задача про кондитерскую Снеговика

Снеговик, работающий в лесной кондитерской, устал пересчитывать мелочь покупателей. Поэтому он решил больше не принимать монеты номиналом 1, 2 и 5 копеек.

Переделать ценники Снеговик не успел. Вместо этого он решил округлять сумму каждой покупки до десятка копеек. Например, если товар стоит 5 рублей и 23 копейки, он возьмёт за него 5 рублей и 20 копеек.

Медведь, Заяц, Белка и Ёж проходили мимо кондитерской Снеговика. Медведь решил угостить друзей свежей выпечкой. Долго уговаривать их не пришлось.

Из меню Медведь выбрал пирог с клюквой за 15 рублей 88 копеек, Заяц захотел мешок медовых пряников за 3 рубля 16 копеек, Белка — мешок орешков со сгущёнкой за 3 рубля 35 копеек, а Ёж предпочёл вафельный торт за 12 рублей 49 копеек.

Когда компания собиралась сделать заказ, Снеговик сообщил им, что не примет к оплате монеты меньше 10 копеек.

Медведь быстро сложил цены выпечки: вся покупка обойдётся в 34 рубля 88 копеек. Придётся округлить эту сумму до 34 рублей 90 копеек и переплатить две копейки.

Медведь решил, что можно разбить заказ и сберечь свои деньги. На сколько покупок нужно его разделить, чтобы сэкономить как можно больше?

Задача про семейный ужин

Каждый Новый год семья Морозовых устраивает праздничный ужин. За столом собираются папа, мама, их сын Петя, дядя Коля, тётя Тома и дедушка. Мама отвечает за организацию праздника. По традиции большой прямоугольный стол накрывают в гостиной с двухместным диваном, одним креслом и тремя стульями. Вот вид комнаты сверху:

Самое сложное в подготовке — придумать план рассадки, ведь у каждого члена семьи есть свои пожелания. Мама заранее выслушала их и составила список:

• Дедушка давно не видел тётю Тому, поэтому хочет сесть напротив неё.
• Петя хотел бы сесть рядом с дедушкой.
• Дядя Коля не хочет сидеть во главе стола.
• У тёти Томы болит спина поэтому она хочет сесть на диван.

Папа всегда сидит во главе стола с левой стороны на кресле, а мама — по левую руку от него на диване.

Получится ли у мамы учесть пожелания всех членов семьи? И где тогда будет сидеть каждый из них?

Важно: считается, что родственники сидят рядом даже в том случае, если их разделяет угол стола.